In the previous column (January/February 2016), we looked at the basic ideas behind control charts and saw how to construct a common X-bar and R chart. In this column we’ll look at two rules that can be used to detect out-of-control situations, and we’ll see why more is not better when it comes to such rules. In the next column we’ll differentiate between being out of control and out of specification—two entirely different concepts.
Figure 1 shows a set of three charts associated with a process. Let’s call it a measurement process, perhaps chromatography, though it could be any quantitative analytical method. We’ll assume that the process has been running consistently for a long time, and the control limits are based on 20 or 30 initial sets of subgroups of data, not on the data shown in Figure 1. The measurement numbers and subgroup numbers all start at “1” in the figure, but these labels are relative to the figure—that is, measurement number 1 in the figure might actually represent the 3169th measurement since the chromatographic method was transferred from the development laboratory to the applications laboratory.
 Figure 1 – A three-sigma rule violation.
Figure 1 – A three-sigma rule violation.The upper chart in Figure 1 is called a run chart or a trend chart. It simply plots the process output (in our case, the integrated peak area for a reference material) as a function of run number—that is, as a function of the sequence order. Because of accuracy requirements for this chromatographic method, the result must fall between the upper specification limit (USL) and the lower specification limit (LSL), shown in red. These might be called method acceptance limits for the chromatographic method to be considered still fit for use. All of the data in Figure 1 lies between these specification limits, so there is no reason to believe the chromatographic method isn’t producing valid results. We’re good to go.
The lowest chart in Figure 1 is a control chart, the familiar R chart in which subgroup ranges are plotted. In this example, the subgroup size is four. These subgroup ranges have been calculated from the data in the run chart at the top, taking the run data four at a time to produce each subgroup range plotted in this R chart. The process appears to be in statistical control as far as the ranges are concerned. Some ranges are larger than others, some ranges are smaller than others, but all of the ranges lie between the control limits. Nothing unusual here.
The middle chart in Figure 1 is the familiar X-bar chart in which subgroup means are plotted. These subgroup means have also been calculated from the data in the run chart at the top, taking the run data four at a time to produce each subgroup mean plotted in this X-bar chart. The process appears to be in statistical control…until we reach subgroup 20, where the subgroup mean plots outside the statistical process control limits. This outlier is unusual!
As we saw in the previous column, the probability that this will happen if the process is behaving now as it has behaved in the past is only 0.00270. So one of two things has happened here: either (a) this is just one of those events that’s expected to happen every now and then, about 3 times in 1000; or (b) the process isn’t behaving now as it has behaved in the past—something is different. Because the probability of (a) is so small, our gut feeling is that possibility (b) is the more likely explanation.
This is called a three-sigma rule violation, where the rule states: A lack of control is indicated when a point falls outside a control limit. Okay, the subgroup mean at subgroup number 20 is a three-sigma rule violation.
What should be done?
We should look for an “assignable cause” and try to remove it. One place to start is in the run chart. Note that the last six points in the run chart (not just the last four) are noticeably and consistently higher in value than most of the previous data points. It looks like the bias of the chromatographic method has shifted—the integrated peak areas have become a bit larger than they’ve been in the past. Why would that be? Well, statisticians can tell you a lot about these charts, but they probably don’t know very much about why things happen in these charts. This is where “profound knowledge” or “domain knowledge” comes in. Translation: we need to talk to a chromatographer to try to find the assignable cause. I’ve done some chromatography, but I don’t consider myself to be a real chromatographer (like Brian Bidlingmeyer,1 for example), so I can only speculate that maybe the lamp in the UV detector has shifted its position because someone bumped the chromatograph…or maybe the instrument manufacturer decided to push a new version of integrator software into the chromatograph, a version they thought was better but was only decidedly different…or maybe…I dunno. At this point I’d call Brian.
It should be said that an assignable cause isn’t always found. Sometimes—about three times in 1000—a “statistical event” occurs, one of those random, “apparently-but-not-really” out-of-control events that happens with a risk of 0.00270. Still, when a rule violation occurs, it’s a good idea to see if you can find an assignable cause, fix it, and try to prevent it from happening again.
Figure 2 shows a run-of-ten rule violation in the R chart, where the rule states: A lack of control is indicated when 10 successive values fall on the same side of the central line. Starting at subgroup number 5, there are 10 ranges that are greater than the central line.
 Figure 2 – A run-of-ten rule violation.
Figure 2 – A run-of-ten rule violation.This might happen if a routine analytical laboratory suffers a loss of personnel, and the remaining analysts are overworked and don’t have time to be as careful as before. This is not good—if the variability is getting to be too large, remedial training might be in order. To be fair, sometimes the rule violation happens the other way—the ranges get smaller. This might happen in a routine analytical laboratory as the analysts become more familiar with the method and their variability decreases. This is good. In either case, if the process has changed and becomes stable in its new state, and the new state is acceptable, you might want to redraw the control limits based on the more current information.
A few statisticians use a run-of-seven rule; probably most statisticians use a run-of-eight rule; some are more conservative and use a run-of-nine rule; I’m even more conservative and use the run-of-ten rule. Why? Because the theoretical risk of triggering a false positive with the run-of-ten rule (0.001953125) is more in keeping with the risk of the three-sigma rule (0.00270) than is the original run-of-eight rule (0.0078125) or the run-of-nine rule (0.00390625). That said, as Wheeler2 points out, Shewhart3 didn’t treat control limits as strict probability limits and split (tiny) hairs like this. Shewhart knew the distributions weren’t always Gaussian (or χ2), weren’t always symmetrical, etc. He didn’t care if the risks were exactly 0.00270—they just needed to be small, so the three-sigma rule and the run-of-eight rule are probably good enough.
One last thing: don’t use too many rules! Beginners soon discover hundreds, perhaps thousands, of specialized rules in the literature. Two familiar examples are found in the Western Electric Statistical Quality Control Handbook:4 Detection Rule Two: A lack of control is indicated when two out of three successive values are: (a) on the same side of the central line and (b) more than two standard deviations away from the central line. Detection Rule Three: A lack of control is indicated when four out of five successive values are: (a) on the same side of the central line and (b) more than one standard deviation away from the central line. Beginners think that if a few rules are good, then more rules must be better. Actually… no. When making multiple, independent statistical decisions, each with its own risk α of giving a wrong answer, the overall risk αEW that at least one of these decisions will give a wrong answer is much bigger than you might think. The relevant equation is:

If, for example, d = 100 rules are used, each with a risk α = 0.003 of being wrong, the overall “experiment-wise” risk (αEW) is equal to:
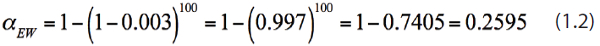
That is, on the average, about every fourth point you plot on each control chart will trigger one of these 100 rules and you’ll think there’s an out-of-control situation when there really isn’t. You’ll waste too much time looking for assignable causes that aren’t there. My advice is to forget all these specialized rules and stick with the three-sigma rule and run-ofwhatever rule only.
“So,” you say, “if my process is out of control, that’s the same as being out of specification. I’d better shut it down.” Not necessarily. Being out of control and being out of specification are two entirely different concepts (hint: look at Figure 1). We’ll talk about this more in the next column.
References
- Bidlingmeyer, B.A.; Deming, S.N. et al. Retention mechanism for reversed-phase ion-pair liquid chromatography. J. Chromatogr. 1979, 186, 419–34.
- Wheeler, D.J. Advanced Topics in Statistical Process Control: The Power of Shewhart’s Charts; SPC Press: Knoxville, Tenn., 1995.
- Shewhart, W.A. Statistical Method from the Viewpoint of Quality Control; Deming, W. Edwards, Ed.; The Graduate School, The Department of Agriculture, Washington, D.C., 1939.
- Small, B. Ed. Western Electric Statistical Quality Control Handbook; Mack Printing Company: Easton, Penn., 1956.
Dr. Stanley N. Deming is an analytical chemist who can be found, as he says, masquerading as a statistician, at Statistical Designs, 8423 Garden Parks Dr., Houston, Texas 77075-4731, U.S.A.; e-mail: [email protected]; www.statisticaldesigns.com