In the past articles, the discussions about methods have always dealt with procedures that estimate sample concentrations over a range of levels. Sometimes, though, all that is needed is a decision about a specification (spec) level. For example, the critical question may be, “Is the amount of the analyte in a sample above or below a set concentration?” In such cases, comparison of each sample’s response with that of the appropriate standard (in matrix) would suffice, ideally. This article looks at the possibilities and pitfalls of such “pass-fail” test procedures.
As with all analytical methods, two basic situations exist. The first is that a true blank is available for the sample matrix in question; in other words, no measurable signal is obtained when the blank is analyzed. The second possibility is that all available matrices are contaminated to at least some (unknown) extent. In both instances, the response at the spec limit may or may not be “well above” the blank’s response, be that response just noise or a positive signal. How to proceed with a pass-fail test depends on which situation applies. Each scenario will be described in turn.
Consider the first (and easier) scenario, where a true blank is available. Here, it is easy to prepare a standard in the blank matrix at the necessary concentration. When analyzed, this solution’s response will be due entirely to the added amount, neglecting noise. If this standard is analyzed multiple times (a minimum of five), the uncertainty associated with the responses can be calculated by: 1) estimating the standard deviation and 2) multiplying by the value of Student’s t corresponding to the degrees of freedom and desired confidence level. If the width of that interval does not contain zero, then the corresponding concentration can be distinguished from a blank. Thus, any sample that does not give a measurable signal can be deemed to be under the spec limit.
What happens if a sample does generate a peak that can be integrated? In such instances, the safest procedure is to analyze the sample five times and determine the uncertainty interval as above. If this new interval does not overlap that of the standard, then the sample can be said to have passed, at the confidence level chosen.
How low can one go with this method? Again, the behavior of the uncertainty interval is the key. If the width includes zero, then the candidate concentration cannot be distinguished from zero (i.e., from a blank).
Unfortunately, it is common to encounter the second scenario (i.e., that a true blank cannot be found). Is it possible to construct a pass-fail test in such situations? The answer is a qualified “Yes,” but quite a bit of judgment calling may be involved.
The first step is to find a matrix that contains as little of the analyte as possible. An aliquot of this material should be diluted until the contaminant level is just low enough to make its response blend into the baseline (i.e., the peak is now too weak to be integrated). Once this dilution factor has been determined, the matrix (in its original state) should be spiked at the spec level; subsequently, the spiked solution should be diluted exactly as was the blank matrix. Thus, the dilution factors for the two samples will be the same. (An alternative approach would be to lower the mass of the solution that is introduced into the instrument until the blank signal vanishes; one possibility is to install a smaller sample loop. However, this strategy results in altering the test equipment and may not be acceptable in some laboratories.)
Next, the diluted spike should be analyzed a minimum of five times and the uncertainty interval calculated, as above. If the interval does not contain zero, then the spike still can be distinguished from zero; the user now is back to the first scenario.
At first blush, this dilution idea may seem “illegal.” However, sample concentrations frequently are altered (i.e., made either higher or lower) before analysis in order to achieve various goals. The rule is that whatever is done to one sample or standard must be done to all. Equal treatment under the law!
Once the reader has accepted the above strategy, he or she is ready to look at an even simpler approach, although it will certainly seem heretical at first! The premise is that postanalysis scaling of the data (e.g., chromatograms) can make the blank’s response “disappear.” Equal treatment under the law then applies to all subsequent data.
The easiest way to explain this idea is to take an actual example. Figure 1 shows an analyte peak in a blank matrix. The scale is such that the analyst can reliably integrate the peak with ease. Figure 2 is the same blank matrix, but spiked at the spec level; the scales on both axes are the same as the corresponding ones in Figure 1.
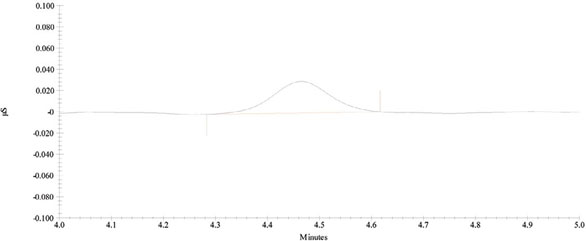
Figure 1 - Analyte’s response in a blank matrix.
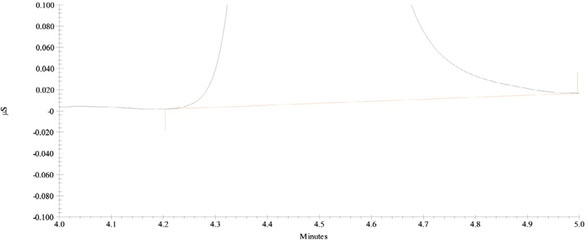
Figure 2 - Analyte’s response after the blank matrix has been spiked at the specification level. Same scale as in Figure 1.
Now compare Figure 3 with Figure 4. The y-axes on both plots have been rescaled identically. Now, the analyte’s response in the blank cannot be distinguished from the baseline. However, the peak in the spike is still large enough to be integrated reliably. Note, though, that the Stop/Start markers on the spike’s peak are closer together than in Figure 2, since the baseline detail is not discernible in the rescaled case.
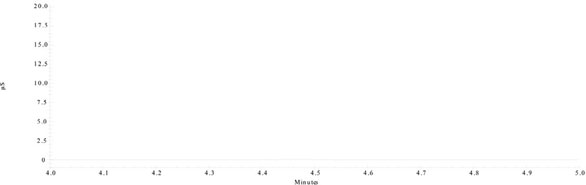
Figure 3 - Same as Figure 1, except the y-axis has been expanded so that the analyte’s response is no longer visible.
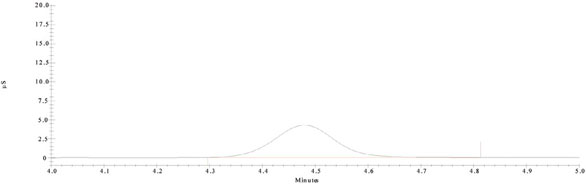
Figure 4 - Same as Figure 2, except the scale on the y-axis is the same as in Figure 3.
The “zoom-out” chromatograms essentially place the analyst back in the first scenario. However, he or she must remember to scale every succeeding chromatogram exactly the same. (This rule actually is no different than the requirement that every sample or standard be diluted or concentrated in the same manner.)
What if the dilution/zooming strategy causes the spike’s peak to disappear as well? In other words, there is no way to get to the luxury of the first scenario. Details will be discussed in the next article.
Mr. Coleman is an Applied Statistician, Alcoa Technical Center, MSTC, 100 Technical Dr., Alcoa Center, PA 15069, U.S.A.; e-mail: [email protected]. Ms. Vanatta is an Analytical Chemist, Air Liquide-Balazs™ Analytical Services, 13546 N. Central Expressway, Dallas, TX 75243-1108, U.S.A.; tel.: 972-995-7541; fax: 972-995-3204; e-mail: [email protected].