Statistical outlier identification and remediation is a topic that has caused issues in almost every laboratory. There are many causes of outliers, including measurement error, sampling error, incorrect recording, or misspecification of the distributional assumptions. When the root cause is not known or cannot be identified easily, statistical methods are employed to identify potential outliers for remediation.
Outliers are defined as observations that appear to be inconsistent with the rest of the data set. A given data set can have more than one outlier, though it is rare in the laboratory setting. Prior to doing any statistical analysis, data should be reviewed and checked for assumptions.
Graphical methods can be used to visually accept assumptions such as normality and the lack of outliers. Some methods include the box plot, histogram, and normal probability plot. Other graphical techniques can be utilized as necessary or appropriate.1
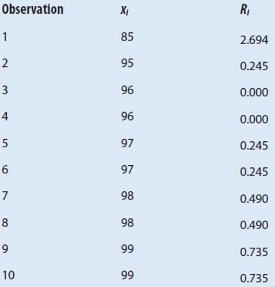
Table 1 – Relative potency
The problem is that outliers can distort and reduce the information contained in the data source or generating mechanism. In the laboratory environment, the existence of outliers will undermine the effectiveness and accuracy of any result generated. Possible outliers are not necessarily bad or erroneous; they just do not reflect the expected outcome of the method. In some situations, an outlier may carry essential information and thus it should be identified for further study.2 Data that are identified as an outlier initially can be shown to be part of the expected distribution once more data are collected. Often they contain valuable information about the process under investigation or the data-gathering and recording process.
Before considering the possible elimination of these points from the data, one should try to understand why they appeared and whether it is likely similar values could be seen in the future. In other words, are these values within the precision and accuracy of the method?
Test for outliers
Once an observation is identified either by graphical or visual inspection as a potential outlier, root cause analysis should begin to determine whether an assignable cause can be found for the spurious result. If no root cause can be determined, and a retest can be justified, the potential outlier should be recorded for future evaluation as more data become available. Removing data points on the basis of statistical analysis without an assignable cause is not sufficient. Statistical significance does not imply causation. Robust or nonparametric statistical methods are alternative methods for analysis. Robust statistical methods such as weighted least-squares regression minimize the effect of an outlier observation.3
Some common tests for outliers are the generalized extreme studentized deviate (GESD) and Dixon Q-test. In practice, the number of outliers in the sample should be small. If there are many outliers in the data set, it ceases to be an outlier detection problem and different approaches are needed.
Generalized extreme studentized deviate
One or more outliers on either side of a normal data set can be detected by using a procedure known as the generalized extreme studentized deviate procedure. The following is the typical procedure for the GESD outlier procedure (see Table 1):
- Determine if a potential outlier exists
- Select a significance level α (Type I error) for the test. Since a Type I error is an incorrect decision, it is desirable to keep it small (i.e., 5%)
- Compute the test statistic:
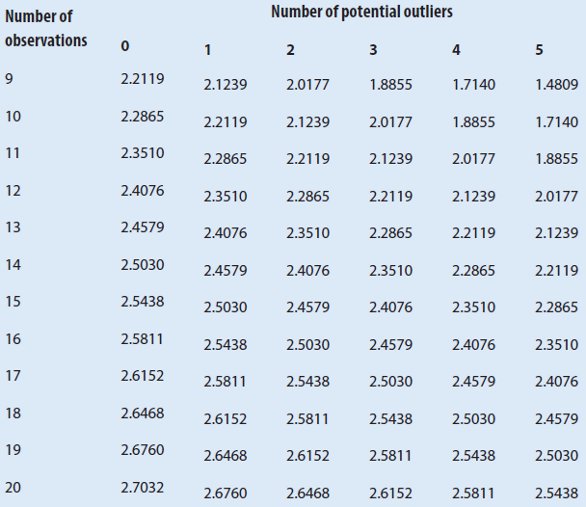
4. Compare the computed value Ri to the table value (see Table 2). Since 2.694 exceeds the tabled value of 2.2865, the value of 85 is considered an outlier.
Table 2 – Critical values for GESD test4
Dixon-type tests
Dixon-type tests are based on the ratio of the ranges. These tests are flexible enough to allow for specific observations to be tested. They also perform well with small sample sizes. Because they are based on ordered statistics, there is no need to assume normality of the data. The following equation is for the largest or smallest observation being an outlier:
If the distance between the potential outlier to its nearest neighbor is large enough, it would be considered an outlier. See Table 3 for the critical values for r10 ratio.
Using the same data from the GESD example, the Dixon Q-test would yield:
The value of r10 is more than the critical value 0.412, implying that 85 is potentially an outlier.
Table 3 – Critical values for Dixon test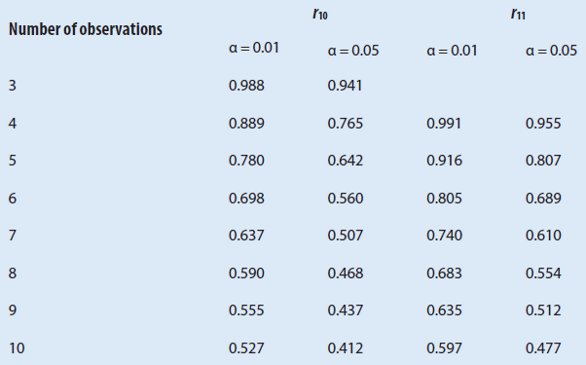
Summary
It is of great importance to identify a sound subset of methods used in the identification and treatment of outliers. The ISO standard 16269:4 gives additional information and tests for the detection of outliers and the remediation methods available.
References
- Tukey, J.W. Exploratory Data Analysis. Addison-Wesley: Reading, MA, 1977.
- ISO 16269:4-2010: Statistical interpretation of data—Part 4: Detection and treatment of outliers.
- Barnett, V.; Lewis, T. Outliers in Statistical Data, 2nd ed.; John Wiley & Sons: New York, NY, 1985.
- Rosner, B. Percentage points for a generalized ESD many-outlier procedure. Technometrics 1983, 25, 165–72.
Steven Walfish, MS, MBA, is President, Statistical Outsourcing Services, 2226 Crossing Way, Wayne, NJ 07470, U.S.A.; tel.: 301-325- 3129; fax: 240-559-0989; e-mail: steven@ statisticaloutsourcingservices.com ; www. statisticaloutsourcing.com